Mathematical Model of LPP:-
The general mathematical model of LPP (or model) with n decision variables and m
constraints can be stated in the following form :
There are some limitations associated with this technique.
These are the following:-
(a) This technique is based on the assumption of linear relations between inputs and
outputs. This means that inputs and outputs can be added, multiplied and divided. But
the relations between inputs and outputs are not always linear. In real life, most of the
relations are non-linear.
(b) The solution of a linear programming problem is also arrived at with such a complicated
method as the ‘simplex method’ which involves a large number of mathematical
calculations.
(c) LP deals with only a single objective, where in real life situations a decision problem
may have conflicting and multiple objectives.
(d) LP model there is no guarantee that decision variables will get the integer value.
METHOD FOR SOLVING LPP
There are two methods for solving the linear programming problem.
(a) Graphical Method
(b) Simplex Method
Graphical Method:– This method is very simple for finding the solution of LPP. But its method
is very difficult to apply when our decisions variables more than two. If decisions variable is
two then we use the graphical method. In graphical method, the extreme point of the feasible
solution space is examined in order to search for the optimal solution that lies at one of
these points.
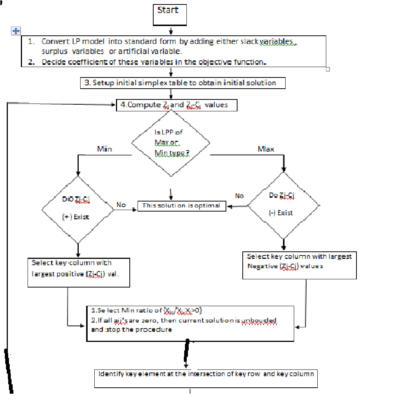
Simplex Method:- The concept of the simplex method is similar to the graphical method. For LP
Problems with several variables, we may not be able to graph the feasible region, but the
optimal solution will still lie at an extreme point of the many sides. The simplex method
examines these extreme points in a systematic manner, repeating the same set of steps of
the algorithm an optimal solution is fine.
It is, for this reason, it is called the iterative method
The name of the algorithm is derived from the concept of a simplex and was suggested by
T.S.Motzkin.
FLOW