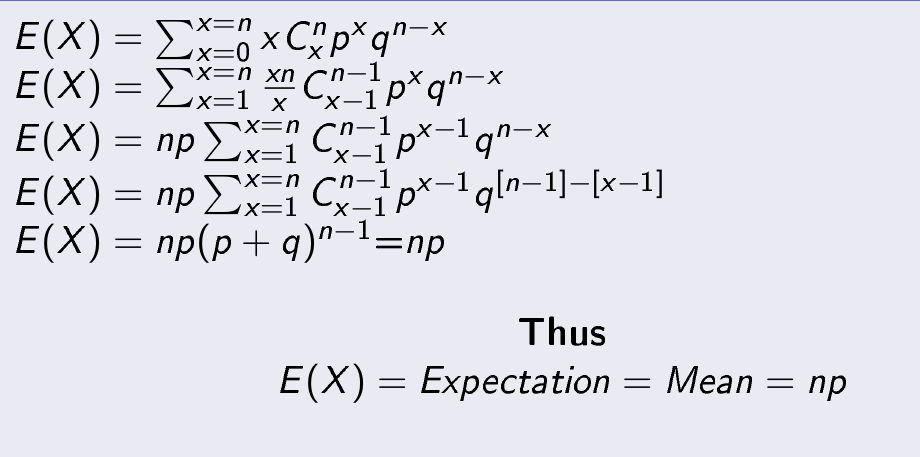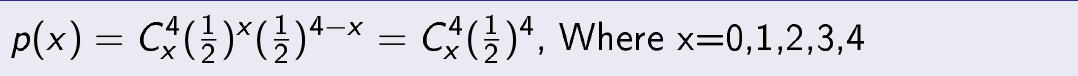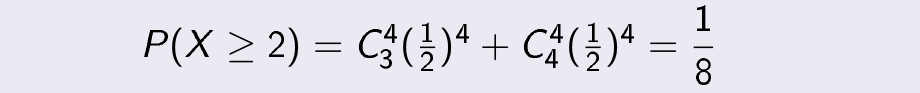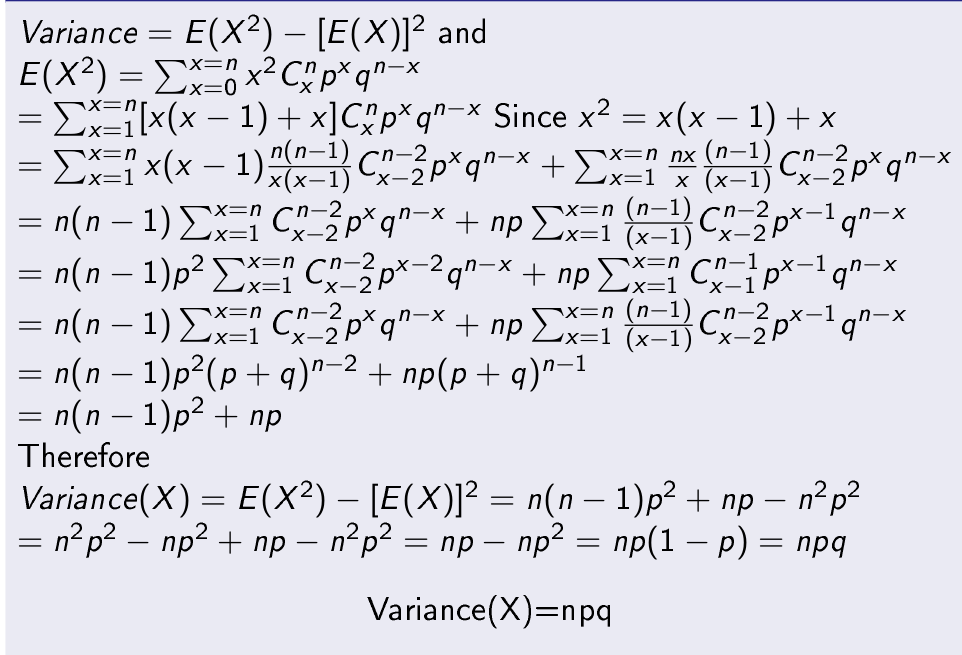Let X be a random variable, it is said to follow binomial distribution if it follows the following probability mass function. And it can have only non-negative values. The binomial distribution is a discrete probability distribution.
Binomial distribution is used to model problems, for instance, getting number of success after certain number of random experiments or trials.
Example-
Problem- If there are four coins which are tossed simultaneously, calculate the probability of getting at least two heads.
Solution-
Probability of getting head of a coin = 1/2
Probability of getting tail of a coin= 1/2
i.e
p=1/2 and q=1/2
probability of getting x heads in trials of 4 coins is
Therefore probability of getting at least two heads are
Mean or Expectation of Binomial Distribution-
Expectation or mean of binomial distributed random variable X is
Variance of binomial distributed random variable X is
Python Code for Binomial Distribution
from scipy.stats import binom
import numpy as np
import matplotlib.pyplot as plt
# Let lambda=np=5
x = np.arange(0,10)
n=50
p=0.10
plt.plot(x, binom.pmf(x, n, p))
plt.savefig(“binom.png”)
Conclusion
In this post, I have explained about binomial distribution. Hope you will understand and apply it.
References
- Fisz, M. and Bartoszyński, R., 2018. Probability theory and mathematical statistics (Vol. 3). J. wiley.
- Sahoo, P., Department of Mathematics University of Louisville Louisville, KY 40