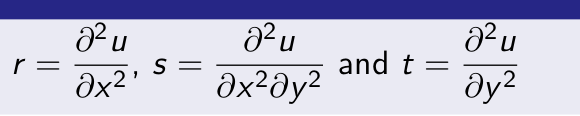If z is a function of two independent variables x and y. Then second order partial differential equation
Rr+Ss+Tt+ f(x,y,z,p,q)=0
Where
r, s and t are
and R, S and T are continuous functions of x and y in domain of xy-plane.
Then if
S2-4RT > 0
Then equation is hyperbolic
S2-4RT= 0
Then equation is parabolic
S2-4RT= 0
Then equation is elliptic
Example-
3 uxx + 6 uxy + 2 uyy = 0
R=3, S= 6 and T=2
And S2-4RT= 36 – 24= 12 >0
Then the equation is hyperbolic.