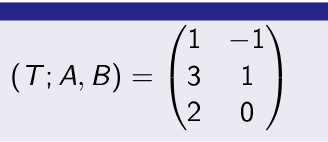Matrix Representation of a Linear Transformation
Suppose U and V are two vector spaces over the same field F of dimensions m and n. Let A = {α1, α2, α 3,……,α3} and B={β1, β2, β3,…….,βn} be ordered bases of U and V.
If T is a linear transformation such that T:U->V and it is defined as
Example-
If a linear transformation which is defined as T(a,b)=(a-b, 3a+b, 2a) from T:V2->V3. Find out the matrix representation linear of a transformation T under the ordered bases
A={(1,0),(0,1)}
B={(1,0,0), (0,1,0), (0,0,1)}.
Solution-
T(1,0) = (1,3,2) = 1 (1,0,0) + 3 (0,1,0) + 2 (0,0,1)
T(0,1) = (-1,1,0)= -1 (1,0,0) + 1 (0,1,0) + 0 (0,0,1)
Then the matrix of linear transformation T:V2->V3 related to ordered bases A and B is
Conclusion-
In this post, I have explained that how to find out matrix under a liner transformation related to ordered bases. Hope you will understand it.