A random variable X is said to follow exponential distribution if it follows the following probability mass function.
Exponential probability distribution is a continuous distribution.
Probability Distribution Function of Exponentially Distributed Variable X
It is heavily used in the Internet traffic modelling and of study queuing models.
Numerical Example-
Problem-
If a computer receives a packet in its interface queue with average 5 milliseconds. Find out that a packet will not wait for more than 15 millisecond.
Solution-
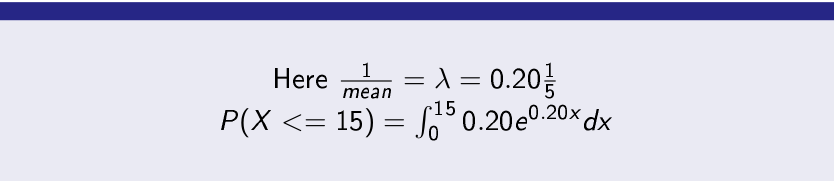Calculate it yourself
Mean or Expectation of Exponential Distributed Variable X
Variance of Exponential Distributed Variable X
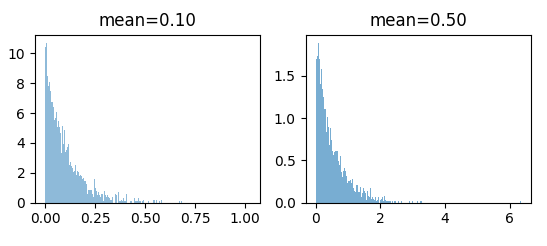
Python Code for Exponential Distribution
import numpy as np
import matplotlib.pyplot as plt
#mean=1/lambda
mean1=0.10
mean2=0.50
y1 = np.random.exponential(mean1, 5000)
y2 = np.random.exponential(mean2, 5000)
plt.subplot(2,2,1)
plt.title(“mean=0.10”)
plt.hist(y1, density=True, bins=500,lw=0,alpha=0.5)
plt.subplot(2,2,2)
plt.title(“mean=0.50”)
plt.hist(y2, density=True, bins=500,lw=0,alpha=0.6)
plt.savefig(“ExponentialDistribution.png”)
Output of the program would be
Conclusion
In this post, I have explained about exponential distribution. Hope you will understand and apply.
References-