Sets
Set is a collection of well-defined objects.
Set’s Representation
Basically, there are two ways of a set representation.
Types of Set
1-Null Set
A set is called null set if it is empty or it does not have any elements and it is denoted by fi.
2-Singelton Set
A set is called singleton if it has only one element or it has a single element.
3-Finite Set
A set having finite number of elements is called finite set.
Example- Set A={1, 4, 7, 10, 15, 17, 20} is a finite set and it has four elements.
4- Sub Set
Suppose there are two sets A={1, 4, 7, 10, 15, 17, 20} and B={1, 4, 7, 10}. Then you can observe that B contains all four elements from A, however, A has seven elements. Then B is set within A and B is called subset of A.
Number of Subsets
If a set having n elements then there will be 2n subsets of the set.
Cartesian Product
Suppose A={1,2,3} B={4, 5, 6} then A ✕ B is Cartesian product of A and B.
A ✕ B = {(1,4),(1,5), (1,6), (2,4),(2,5), (2,6), (3,4),(3,5), (3,6)} which is set of ordered pairs of elements of A and B.
A ✕ B ≠ B ✕ A
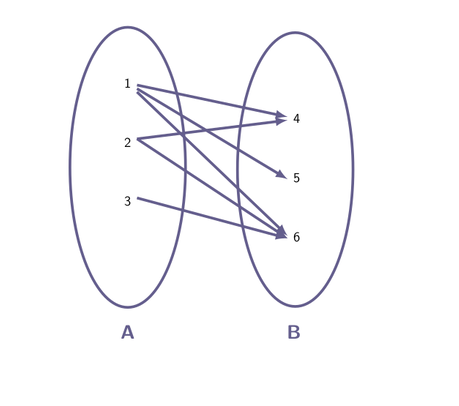
Binary Relation
A binary relation is a subset of Cartesian product A ✕ B. Which establishes relation between elements of A and B.
For example, If we say elements of A divides B in A ✕ B = {(1,4),(1,4), (1,6), (2,4),(2,5), (2,6), (3,4),(3,5), (3,6)}.
Then the relation will be
R={(1,4),(1,5), (1,6),(2,4), (2,6), (3,6) }
The relation can be written as 1R4, 1R5, 1R6, 2R4, 2R6 and 3R6. Here R means “divides”.
Types of Relation-
Basically, there are three types of relations.
Reflexive Relation
A relation R on a set A={1,2,3} is said to be reflexive if an element of the set A relates itself.
For example an “equal to” relation on A ✕ A = {(1,1),(1,2)(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}
And R={(1,1),(2,2),(3,3)} 1=1, 2=2 and 3=3 i.e aRa
Symmetric Relation
A relation is said to be symmetric if aRb then bRa. “Equal to” is a symmetric relation because a=b then b=a.
Transitive Relation
A relation is said to be transitive is aRb and bRc then aRc. “Equal to” is transitive relation because if a=b and b=c the a=c.
“Greater than” is a transitive relation if a>b and b>c then a>c.
Equivalence Relation
A binary relation is called equivalence relation if it is reflexive, symmetric and transitive.
Example is “equal to”
Parallel relation for straight lines is an equivalence relation.