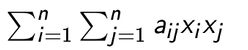Quadratic Form in Linear Algebra

Quadratic Form in Linear Algebra

An expression

is called quadratic form in the variables x₁, x₂, x₃,………….,x_n over field F.

Where a_ij i=1,2,3,….n, j=1,2,3,….m are elements of F.

If a_ij are real then quadratic form is called real quadratic form.

Examples of Quadratic Form

1-x₁²+x₂²+ 6 x₁ x₂ is a quadratic form in variables x₁ and x₂.

2- x₁² + 2x₂² + 3x₃² + 4x₁ x₂-6 x₂ x₃ +8 x₃ x₁ is a quadratic form in three variables x₁, x₂ and ₃.

Quadratic Form’s Matrix

expression is  a quadratic form in variables x₁, x₂, x₃,……, x_n and X={x₁, x₂, x₃,……, x_n} then there exists a symmetric matrix A such that
f= X^TAX. Here A is said to be matrix of quadratic form.

Examples-
Matrix of the quadratic form in two variables is  x₁²+x₂²+ 6 x₁ x₂    the matrix will be.

Matrix of the quadratic form in three  variables is x₁² + 2x₂² + 3x₃² + 4x₁ x₂-6 x₂ x₃ +8 x₃ x₁ the matrix will be.

Quadratic Form’s Classification

expression is  a quadratic form in variables x₁, x₂, x₃,……, x_n      the quadratic form f is said to be.

1- Positive Definite

If the value of f>0 for all x₁, x₂, x₃,……, x_n.
And f=0 if x₁= x₂= x₃,……,= x_n = 0.

2- Positive Semi-Definite

If the value of f>0 for all x₁, x₂, x₃,……, x_{n.
And also f=0 if some vectors from x1, x2, x3,……, xn are not zero.}

3- Negative Definite

If the value of f< 0 for all x₁, x₂, x₃,……, x_{n.
And f=0 if x1= x2= x3,……,= xn=0}

4-Negative Semi-Definite

If the value of f<0 for all x₁, x₂, x₃,……, x_{n.
And also f=0 if some vectors from x1, x2, x3,……, xn are not zero.}

5- Indefinite

A quadratic form f is called indefinite if values of f is positive as well as negative for variables x₁, x₂, x₃,……, x_n.

Classification of a Quadratic Form Based on Eigen Values

Quadratic form f= X^TAX is said to be.

1- Positive definite if all eigen values of matrix A are positive.
2-Negative definite if all eigen values of matrix A are negative.
3- Positive semi-definite if eigen values matrix A are positive and at least one is zero.
4- Negative semi-definite if eigen values matrix A are negative and at least one is zero.
5- Indefinite if eigen values of matrix A are both positive and negative.

Example-

Suppose a quadratic expression is x₁² + x₂² + 0 x₃² then its matrix A and eigen values are 3, 4, 0 which are calculated below.

At least one eigen value is zero and others all eigen values are positive then matrix is positive semi-definite.

Conclusion-

In this post I have explained about  quadratic form which have a lot of application in various domains. Hope you will understand and apply.